Skip to content

The simplex method

simplex method 从一个 basic feasible solution 沿着边到另一个 basic feasible solution, 永远往 cost reducing 方向走, 直到到达 optimal solution.

本章考虑下列 standard form problem:

\[\begin{array}{rcl}\mathrm{minimize}&\mathbf{c^{\prime}x}\\\mathrm{subject~to}&\mathbf{Ax}=\mathbf{b}\\&\mathbf{x}\geq\mathbf{0},\end{array}\]

令 \(P\) 为相应的 feasible set, 假设 \(\mathbf{A}\) 为 \(m \times n\) 矩阵并且 row vectors 线性无关, 用 \(\mathbf{A}_{i}\) 和 \(\mathbf{a}_{i}'\) 分别表示 column 和 row.

Optimality conditions

因为是 minimizing a convex function over a convex set, 所以 LP 的 locally optimal solution 就是 globally optimal solution.

feasible direction

Let \(\mathbf{x}\) be an element of a polyhedron \(P\). A vector \(\mathbf{d} \in \mathfrak{R}^n\) is said to be a feasible direction at \(\mathbf{x}\), if there exists a positive scalar \(\theta\) for which \(\mathbf{x} + \theta \mathbf{d} \in P\).

假设 \(\mathbf{x}\) 是一个 basic feasible solution, \(B(1), B(2), \dots, B(m)\) 为 basic variables 的下标, 令 \(\mathbf{B}=[\mathbf{A}_{B(1)}, \dots, \mathbf{A}_{B(m)}]\) 为对应的 basis matrix. 特别地, 每个 nonbasic variables 都有 \(x_{i}=0\), 令 vector \(\mathbf{x}_{\mathbf{B}}=\left(x_{B(1)}, \dots, x_{B(m)}\right)\), 显然有

\[ \mathbf{x}_{\mathbf{B}} = \mathbf{B}^{-1}\mathbf{b}. \]

想要到达另一个 basic feasible solution, 显然我们需要增大某个 nonbasic variable \(x_j\), 不妨令其他的 nonbasic variable 不变, 然后令 \(d_{j}=1\). 类似地, 我们定义 \(\mathbf{d}_{\mathbf{B}}\), 接着推导要使 \(\mathbf{x}+\theta \mathbf{d}\) 为 basic feasible solution 的条件.

显然我们需要 \(\mathbf{A}(\mathbf{x}+\theta \mathbf{d})=\mathbf{b} \to \mathbf{A}\mathbf{d}=\mathbf{0}\), 即

\[ \mathbf{0}=\mathbf{Ad}=\sum_{i=1}^{m}\mathbf{A}_{B(i)}d_{B(i)} + \mathbf{A}_{j}d_{j} = \mathbf{B}\mathbf{d}_{\mathbf{B}} + \mathbf{A}_{j} \]

因此 \(\mathbf{d}_{\mathbf{B}}=-\mathbf{B}^{-1}\mathbf{A}_{j}\). 接下来我们称上述条件的 \(\mathbf{d}\) 为 \(j\)th basic direction, 要使 \(\mathbf{x}+\theta \mathbf{d}\) 是 feasible 的还需要满足 \(\mathbf{x}+\theta \mathbf{d} \geq \mathbf{0}\). 显然我们只需要考察 \(\mathbf{x}_{\mathbf{B}}+\theta \mathbf{d}_{\mathbf{B}}\), 若 \(\mathbf{x}_{\mathbf{B}} > \mathbf{0}\), 那么无论 \(\mathbf{d}_{\mathbf{B}}\) 取何值我们都能控制 \(\theta\) 来令 \(\mathbf{x}_{\mathbf{B}}+\theta \mathbf{d}_{\mathbf{B}} > 0\), 但是由于 degeneracy 的存在, 我们需要分两种情况考虑:

  1. \(\mathbf{x}\) is nondegenerate: 那么显然 \(\mathbf{d}\) 是 feasible direction.
  2. \(\mathbf{x}\) is degenerate: 此时存在走到 infeasible solution 的可能.
Example

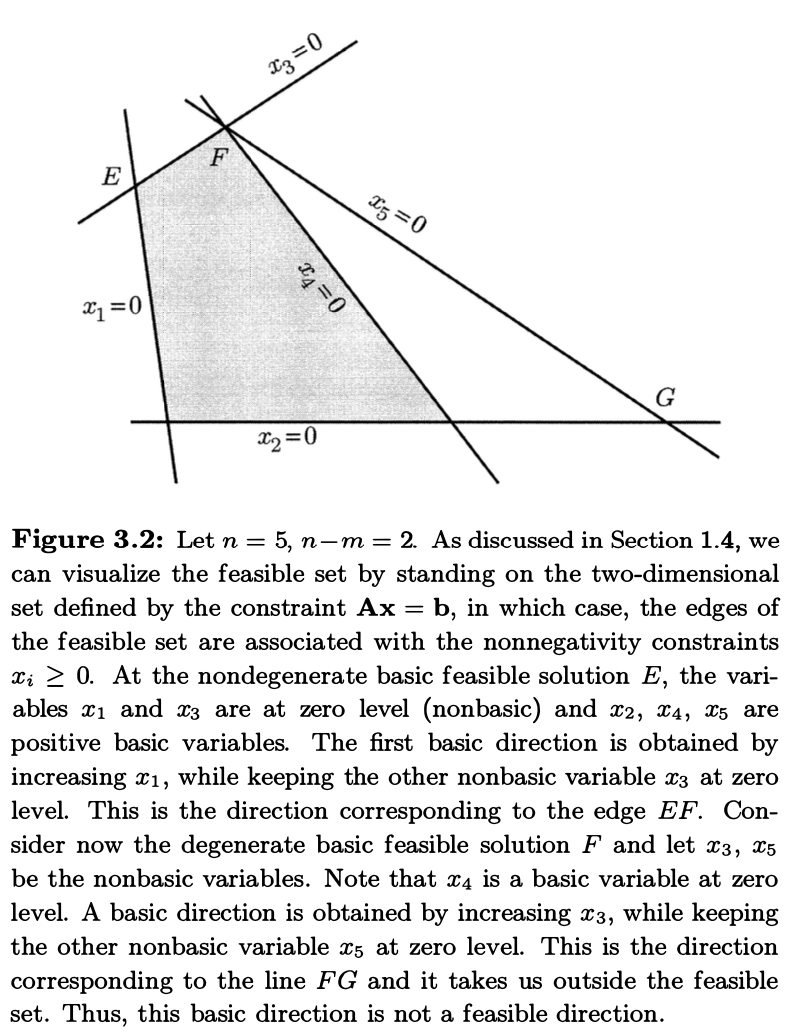
image.png

接着我们考察 \(\mathbf{c'x}\) 的变化. 此时 \(\mathbf{c'x} \to \mathbf{c}'\mathbf{x}+\theta \mathbf{c}'\mathbf{d}\), 而 \(\mathbf{c}'\mathbf{d}=\sum_{i=1}^{m}c_{i}d_{i}+c_{j}d_{j}=c_{j}-\mathbf{c}_{\mathbf{B}}'\mathbf{B}^{-1}\mathbf{A}_{j}\), 直觉上来说, 我们可以将 \(c_{j}\) 看作移动 \(d_{j}\) 的代价, 而 \(\mathbf{c}_{\mathbf{B}}'\mathbf{B}^{-1}\mathbf{A}_{j}\) 则是这个移动的补偿.

reduced cost

Let \(\mathbf{x}\) be a basic solution, let \(\mathbf{B}\) be an associated basis matrix, and let \(\mathbf{c}_{\mathbf{B}}\) be the vector of costs of the basic variables. For each \(j\), we define the reduced cost \(\bar{c_{j}}\) of the variable \(x_{j}\) according to the formula

\[\bar{c_{j}}=c_{j} - \mathbf{c}_{\mathbf{B}}'\mathbf{B}^{-1}\mathbf{A}_{j}.\]

由 \(\mathbf{B}\) 的定义可以知道 \(\mathbf{B}^{-1}[\mathbf{A}_{B(1)} \cdots \mathbf{A}_{B(m)}]=\mathbf{I}\), 特别地, 我们有 \(\mathbf{B}^{-1}_{i}\mathbf{A}_{B(i)}=\mathbf{e}_{i}\). 因此对于每个 basic variable \(x_{B(i)}\), 我们有

\[ \bar{c}_{B(i)} = c_{B(i)} - \mathbf{c}'_{\mathbf{B}}\mathbf{e}_{i}=c_{B(i)}-c_{B(i)}=0 \]

由此我们可以知道 basic variable 的 reduced cost 为 0.

Theorem

Consider a basic feasible solution \(\mathbf{x}\) associated with a basis matrix \(\mathbf{B}\), and let \(\bar{\mathbf{c}}\) be the corresponding vector of reduced costs.

  1. If \(\bar{\mathbf{c}}\geq \mathbf{0}\), then \(\mathbf{x}\) is optimal.
  2. If \(\mathbf{x}\) is optimal and nongenerate, then \(\bar{\mathbf{c}} \geq \mathbf{0}\).
Note

当 \(\mathbf{x}\) 是一个 degenerate 的 optimal solution 时, 可能存在 \(\bar{c}_{j}<0\), 也就是说 optimal solution 不唯一. 反过来, 当 \(\mathbf{x}\) 是 nondegenerate 的时, optimal solution 唯一.

optimal basis matrix

A basis matrix \(\mathbf{B}\) is said to be optimal if:

  1. \(\mathbf{B}^{-1}\mathbf{b} \geq \mathbf{0}\), and
  2. \(\bar{\mathbf{c}}'=\mathbf{c}'-\mathbf{c}'_{\mathbf{B}}{\mathbf{B}}^{-1}\mathbf{A} \geq \mathbf{0}'\).

Development of the simplex method

首先假设所有 basic feasible solution 都是 nondegenerate 的.

假设现在在 basic feasible solution \(\mathbf{x}\), 并且求出了所有 nonbasic variables 的 reduced costs \(\bar{c}_{j}\):

  • 如果他们都是非负的, 说明 \(\mathbf{x}\) 是 optimal solution, 停止算法.
  • 若 nonbasic variable \(x_{j}\) 对应的 \(\bar{c}_{j} < 0\), 说明 \(j\)th basic direction \(\mathbf{d}\) 是 cost 减少的 feasible direction, 我们沿着 \(\mathbf{d}\) 走, \(x_{j}\) 会从 0 变成正数而其它 nonbasic variables 保持为 0, 这种情况就称为 \(x_{j}\) (or \(\mathbf{A}_{j}\)) enters or is brought into the basis.

由于 basic variables 的值会改变, 我们需要保证他们满足 \(\mathbf{x} \geq \mathbf{0}\) 的条件, 因此设 \(\theta^{\ast} = \max\{\theta \geq 0 \vert \mathbf{x} + \theta \mathbf{d} \in P\}\), 此时减少的 cost 为 \(\theta^{\ast}\bar{c}_{j}\), 根据 \(\mathbf{d}\) 的正负性分两种情况:

  • \(\mathbf{d} \geq \mathbf{0}\), 此时任意 \(\theta \geq 0\), 都有 \(\mathbf{x}+\theta \mathbf{d} \geq \mathbf{0}\), 因此 \(\theta^{\ast} = \infty\), minimum cost 为 \(-\infty\)
  • 存在某些 \(i\) 使得 \(d_{i} < 0\), 于是有 \(\theta^{\ast} = \min_{\{i \vert d_{i} < 0\}}\left( -\frac{x_{i}}{d_{i}} \right)\), 只需要考虑 basic variables, 因此上式等价于
    \(\(\theta^{\ast}=\min_{\{i=1,\dots,m\vert d_{B(i)}<0\}}\left( -\frac{x_{B(i)}}{d_{B(i)}} \right).\)\)

确定好 \(\theta^{\ast}\) 后, 我们移动到新的 feasible solution \(\mathbf{y} = \mathbf{x} + \theta^{\ast}\mathbf{d}\). 设 \(\ell\) 为能取到 \(\theta^{\ast}\) 的下标之一, 于是有 \(d_{B(\ell)} < 0\) 和 \(x_{B(\ell)} + \theta^{\ast}d_{B(\ell)} = 0\). 此时 \(x_{B(\ell)}\) 变成了 0, 而 nonbasic variable \(x_{j}>0\), 将 \(\mathbf{B}\) 中的 \(\mathbf{A}_{B(\ell)}\) 用 \(\mathbf{A}_{j}\) 替换得到

\[\overline{{\mathbf{B}}}=\left[\begin{array}{ccccccc}|&&|&|&|&&|\\\mathbf{A}_{B(1)}&\cdots&\mathbf{A}_{B(\ell-1)}&\mathbf{A}_{j}&\mathbf{A}_{B(\ell+1)}&\cdots&\mathbf{A}_{B(m)}\\|&&|&|&|&&|\end{array}\right]\]
Theorem
  1. The columns \(\mathbf{A}_{B(i)}, i\not= \ell\), and \(\mathbf{A}_{j}\) are linearly independent and, therefore, \(\overline{\mathbf{B}}\) is a basis matrix.
  2. The vector \(\mathbf{y} = \mathbf{x} + \theta^{\ast}\mathbf{d}\) is a basic feasible solution associated with the basis matrix \(\overline{\mathbf{B}}\).
Proof

TODO

令 \(\mathbf{u} = -\mathbf{d}_{B} = \mathbf{B}^{-1}\mathbf{A}_{j}\).

An iteration of the simplex method
  1. In a typical iteration, we start with a basis consisting of the basic columns \(\mathbf{A}_{B(1)}, \dots, \mathbf{A}_{B(m)}\), and an associated basic feasible solution \(\mathbf{x}\).
  2. Compute the reduced costs \(\bar{c}_{j} = c_{j} - \mathbf{c'}_{B}\mathbf{B}^{-1}\mathbf{A}_{j}\) for all nonbasic indices \(j\). If they are all nonnegative, the current basic feasible solution is optimal, and the algorithm terminates; else, choose some \(j\) for which \(\bar{c}_{j} < 0\).
  3. Compute \(\mathbf{u} = \mathbf{B}^{-1}\mathbf{A}_{j}\). If no component of \(\mathbf{u}\) is positive, we have \(\theta^{\ast}=\infty\), the optimal cost is \(-\infty\), and the algorithm terminates.

  4. If some component of \(\mathbf{u}\) is positive, let
    \(\(\theta^{\ast}=\min_{\{i=1,\dots,m\vert u_{i}>0\}}\frac{x_{B(i)}}{u_{i}}.\)\)

  5. Let \(\ell\) be such that \(\theta^{\ast}=x_{B(\ell)} / u_{\ell}\). Form a new basis by replacing \(\mathbf{A}_{B(\ell)}\) with \(\mathbf{A}_{j}\). If \(\mathbf{y}\) is the new basic feasible solution, the values of the new basic variables are \(y_{j} = \theta^{\ast}\) and \(y_{B(i)} = x_{B(i)} - \theta^{\ast}u_{i}, i\not= \ell\).

simplex method 在 nondegenerate 情况下可以正确运行并在有限次 iterations 后终止:

Theorem

Assume that the feasible set is nonempty and that ev­ery basic feasible solution is nondegenerate. Then, the simplex method terminates after a finite number of iterations. At termination, there are the following two possibilities:

  1. We have an optimal basis \(\mathbf{B}\) and an associated basic feasible solution which is optimal.
  2. We have found a vector \(\mathbf{d}\) satisfying \(\mathbf{Ad}=\mathbf{0}\), \(\mathbf{d} \geq \mathbf{0}\), and \(\mathbf{c'}\mathbf{d} < 0\), and the optimal cost is \(-\infty\).

The simplex method for degenerate problems

当存在 degeneracy 时, 可能会遇到两种情况:

  1. 若当前 basic feasible solution \(\mathbf{x}\) 是 degenerate 的, 同时某些 basic variables \(x_{B(\ell)}=0\) 以及 \(d_{B(\ell)} < 0\), 那么此时 \(\theta^{\ast}=0\), 新的 basic feasible solution 与原来的相同. 但我们依然可以通过将 \(\mathbf{A}_{B(\ell)}\) 替换为 \(\mathbf{A}_{j}\) 定义 \(\overline{\mathbf{B}}\) 开启下一轮 iteration.
  2. \(\theta^{\ast}>0\) 时仍然可能会有多个 basic variables 变成 0 的情况, 而离开 basis 的只会有一个, 因此得到新的 basic feasible solution 依然时 degenerate 的.

原地进行 basis change 可以进入下一轮迭代继而找到一个 cost reducing feasible direction, 但是也有可能回到最初的 basis 造成 cycling.

Pivot Selection

simplex 算法中选择 \(\bar{c}_{j} < 0\) 的 \(j\) 和多个取到 \(\theta^{\ast}\) 的 \(\ell\) 时都具有一点自由度, 而做出这些选择的规则被称为 pivoting rules.

对于 pivoting rules, 有一些符合直觉的原则:

  1. 选择 \(\bar{c}_{j}\) 最小的 \(j\). 但是最终减少的 cost 还与我们能在这个方向上移动多远有关, 于是有下一则 rule.
  2. 选 \(\theta^{\ast}\lvert \bar{c}_{j} \rvert\) 最大的 \(j\), 对于每一个可能的 \(j\), 我们都需要遍历所有 basic variables 来计算它的 \(\theta^{\ast}\), 总的运行时间实际并不见得有减少.

对 large problems, 即便是选择最小的 \(\bar{c}_{j}\) 都可能 computationally expensive. 在实践中, 有时会采用一些简单的 rules, 例如 smallest subscript rule, 即选择下标最小的 \(j\). 也有一些基于 candidate lists 的 rule 能改进整体的 running time 的 rules, 例如 steepest edge rule 和 Devex.

选择 exiting column 最简单的 rule 是 smallest subscript, 若选择 entering 和 exiting column 时都选择 smallest subscript 可以避免 cycling.

Implementations of the simplex method

在 simplex method 中, \(\mathbf{B}^{-1}\mathbf{A}_{j}\) 起到关键作用.