Lec 7
Introduction¶
Definition 1.
A metric space is a pair \((X,d)\), where \(X\) is a set, and \(d: X \times X \to R\) is the distance function (also referred to as the metric), which satisfies the following conditions:
- For all \(x,y \in X \, d(x,x) = 0\) and if \(x \neq y, d(x,y) = d(y,x) >0\).
- Triangle inequality: for all \(x,y,z \in X, d(x,y) \leq d(x,z) + d(z,y)\).
Example 2.
考虑 \(\ell_{p}\) metric space \(\left(\mathbb{R}^{k}, d_{p}\right)\), 其中
- 当 \(p=2\) 时,\(d_{p}\) 即为 Euclidean distance;
- 当 \(p=1\) 时,\(d_{p}\) 也被称为 Manhattan distance;
- 当 \(p < 1\) 时,对于 \(k \geq 2\) 的情况,\(d_{p}\) 不满足 triangle inequality.
- 此时,对于任意整数 \(k \geq 2\), 都存在反例 \(x=(1,0,\dots,0), y=(0,1,\dots,0), z=(0,0,\dots,0) \in \mathbb{R}^{k}\) 使得 \(d_{p}(x,y) = 2^{1/p} > d_{p}(x,z) + d_{p}(y,z) = 2\).
Note
当 \(1 \leq p < \infty\) 时,\(d_{p}\) 满足 triangle inequality 的形式即 Minkowski inequality.
Example 3.
给定包含 \(n\) 个点且边权为正的图 \(G\), 它对应的 graph metric 为 \((V,d)\), 其中 \(V\) 为点集,\(d(x,y)\) 定义为图 \(G\) 中点 \(x\) 到 \(y\) 的最短路。
任意 finite metric (即 \(X\) 为有限集合的 metric \((X,d)\)) 都可以被表示为以 \(X\) 为点集的完全图 \(G\) 对应到 graph metric.
Low-Distortion Embeddings¶
对于 \(\ell_{p}\) metric spaces, 尤其是 \(\ell_{1}, \ell_{2}\) 和 \(\ell_{\infty}\), 由于已经存在一些能很好利用其 geometry 特性的算法,因此在处理其他 metric space 时,一个很自然的想法是将其 embed 到另一个简单的 metric space 上处理,同时保证在相同的两点之间的 distance 保持不变。
能保证 distance 完全不变的 embedding 被称为 isometric embedding: 给定 metric spaces \((X,d_{X})\) 和 \((Y,d_{Y})\), 存在 map \(f \colon X \to Y\), 使得 \(d_{X}(x, x') = d_{Y}(f(x), f(x')), \forall x, x' \in X\). 例如,对于任意 \(n\) point metric space \(X=\{ x_{1}, x_{2}, \dots, x_{n} \}\) with metric \(d\), 由于三角形两边之差小于第三条,存在 isometric embedding \(f(x)=\left( d(x,x_{1}), d(x,x_{2}), \dots, d(x,x_{n}) \right)\) 能将 \((X,d)\) 映射到 \((\mathbb{R}^{n}, d_{\infty})\).
isometric embedding 并不总是存在,例如 metric \(d\) 满足 \(d(x,y)=d(y,z)=d(z,w)=d(x,w)=1, d(x,z)=d(y,w)=2\) 且 \(X=\{ x,y,z,w \}\) 的 metric space \((X,d)\) 不存在到 \(\ell_{2}\) 的 isometric embedding.
因此,当 distance 不能保持完全一致的情况可以考虑 approximately 一致,这通过对 embedding 添加 distortion 来达到。
Definition 4.
Given two metric spaces \((X,d)\) and \((Y,d')\), and some function \(f \colon X \to Y\), we say that \(f\) is an embedding of \((X,d)\) into \((Y,d')\) with distortion \(\alpha \geq 1\) if there is a scaling factor \(\beta\) such that for all \(x,y \in X\), it holds that \(\beta \cdot d(x,y) \leq d'(f(x),f(y)) \leq \alpha \beta \cdot d(x,y)\). And we say that \((X,d)\) can be embedded into \((Y,d')\) with distortion \(\alpha\) if such a function \(f\) exists.
Bourgain's Embedding¶
Theorem 1.
Given any finite metric \((X,d)\) with \(\lvert X \rvert=n\), there exists an embedding of \((X,d)\) into \(\mathbb{R}^{k}\) under the \(\ell_{1}\) distance metric (actually, any \(\ell_{p}\) metric), where \(k=O(\log^{2}n)\), and the distortion of the embedding is \(O(\log n)\).
Remark 5.
\(O(\log n)\) 的 distortion 已经是最优结果,但是 dimension \(k\) 还可以优化到 \(O(\log n)\)1.
Theorem 1 通过构造一个满足条件的 randomized embedding 证明。构造过程如下:记 \(S_{i,j} \subset X\) for \(i \in \{ 1,2,\dots,\log n \}\) 以及 \(j \in \{ 1,\dots,c\log n \}\), 其中 \(c\) 为常数。对于每个 \(S_{i}\), 所有点以 \(\frac{1}{2^i}\) 的概率选入,一共求出 \(c\log n\) 个这样的 \(S_{i}\), 因此任意集合 \(S_{i,j}\) 都有 \(\mathbf{E}[\lvert S_{i,j} \rvert] = n / 2^i\). 接着,\(f: X \to \mathbb{R}^{k}\) 定义如下
其中,\(d(x,S)=\min_{y \in S}d(x,y)\).
Possible Intuition
考虑最简单的情形:\(f : V \to \mathbb{R}\), 即 \(f(x)\) 为 \(x\) 到某一点 \(x'\) 的距离 \(d(x, x')\). 若每个点 \(x\) 都指定一个确定的 \(x'\), 显然这样很难让所有可能的点对 \((x,y)\) 都满足 low-distortion, 完全随机指定 \(x'\) 也是一样,单个的 \(x'\) 若要应付 \(n\) 个可能的点对则灵活性太小。
不妨考虑用点集 \(S\) 来应付所有点对 \((x,y)\), 令 \(f(x)=d(x, S) := \min_{x' \in S}d(x, x')\), 让每个 \(x\) 都拥有一个 \(x'\) 的情况下引入有限制(\(x'\) 是 \(S\) 中离 \(x\) 最近的点)的随机性。对于点对 \((x,y)\), 此时 mapping 可能如下2:

可以发现,\(f\) 是 non-expanding 的:\(\lvert f(x) - f(y) \rvert \leq d(x, y), \forall x,y \in X\), 我们只需证明(或者稍作修改令)\(f\) 也是 not-too-shrinking 的即可:\(\lvert f(x) - f(y) \rvert \geq \Delta, \forall x, y \in X\).
在下图2中,有 \(d(x, S) \leq \delta, d(y, S) \geq \delta + \Delta\), 于是 \(\lvert f(x) - f(y) \rvert \geq \Delta\) 显然满足 not-too-shrinking:
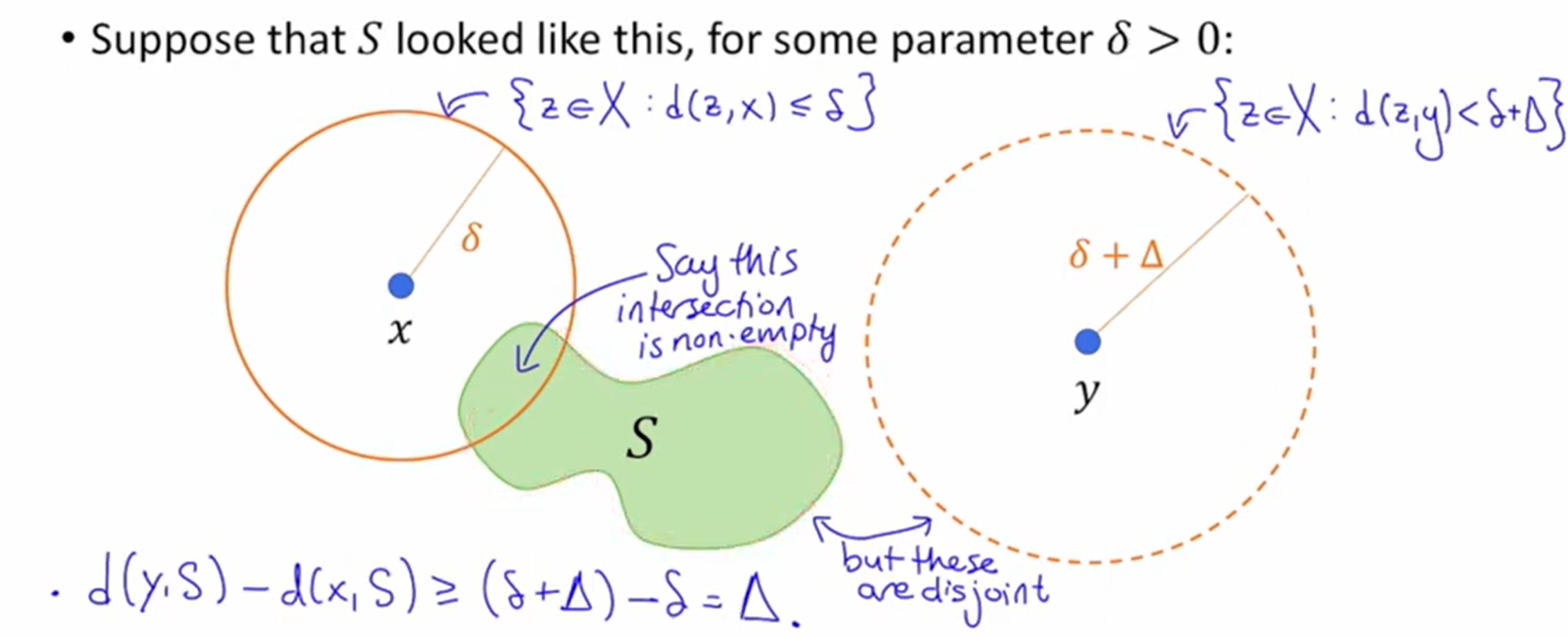
Note
这种以某点 \(x\) 为圆心,\(r\) 为半径画圆进行分析的技巧在 散点 + 考虑 distance 的问题中很好用,例如 k-Suppliers.
由于 \(S\) 的选取可以很灵活,对于 \(d(x,y)\) 较大的点对,可以令 \(S\) 密度大一点并多次采样提高成功率,对于 \(d(x,y)\) 较小的点对则令 \(S\) 密度小一点,这样就能高概率得到上图的情形。
具体而言,设 \(S\) 的 size 大致为 \(2, 4, \dots, n\) 共有 \(\log n\) 档,每个 size 都取样 \(k\) (\(k\) 为 redundancy, 取值由最后使用 Chernoff bounds 进行 union bound 时决定) 次,最后共 \(k\log n\) 个 \(S\), 然后令 \(f(x)=\left( d(x,S_{1,1}), d(x, S_{1,2}), \dots, d(S_{\log n, k}) \right)\), non-expanding 是必然满足的,而 由于只有一部分 \(S\) 可以满足 not-too-shrinking, 且 \(\lvert f(x)-f(y) \rvert\) 会将所有 \(S\) 的结果求和,所以 distortion 会有一定损失。
Sparsest Cuts¶
Warm-Up
Let \(G=(V,E)\) be a weighted, undirected graph, on \(n\) vertices with edge weights \(w_{uv}\) on the edge \(\{ u,v \} \in E\). Let \(d: V \times V \to \mathbb{R}\) be the associated graph metric.
Explain how to efficiently find and apply a map \(f: V \to \mathbb{R}^{k}\), for \(k = O(\log^2 n)\), so that
holds with high probability. Above, \(V \choose 2\) refers to the set of alll unordered pairs \(\{ u,v \}\) for \(u,v \in V\) and \(u \neq v\).
直接套 Bourgain's embedding 就完事了。
对于图 \(G=(V,E)\), 定义 cut \((S, \bar{S})\) 的稀疏程度为
以及图 \(G\) 的稀疏程度
其中 \(\bar{S} \coloneqq V / S\) 为 \(S\) 的补集,\(E(S, \bar{S})\) 为一端在 \(S\) 一端在 \(\bar{S}\) 的边集。
找到 \(S\) 来最小化 \(\phi(G)\) 在 clustering 中很有用,但是这个问题是 NP-hard 的,因此考虑 randomized approximation algorithm, 接下来我们将会找到 \(S\) 使得 \(\phi(S, G) \leq O(\log n)\phi(G)\).
Note
想要找到一个满足 \(\alpha\) 为常数的 \(\alpha\)-approximation algorithm 也是 NP-hard 的,因此 \(O(\log n)\)-approximation 已经是一个相当优秀的结果了。
Connection to Metrics¶
下面将证明
其中 minimum 部分是在所有函数 \(f : V \to \mathbb{R}^{k}\) for some \(k\) 中寻找最小值。
Q1
Show that
where the minum is over all functions \(f: V \to \{ 0,1 \}\) so that \(f\) takes on both values \(0\) and \(1\).
Hint
What's a natural way to relate a set \(S \subseteq V\) to a function \(f : V \to \{ 0,1 \}\)?
令
此时 \(\sum_{\{ u,v \} \in E} \lvert f(u) - f(v) \rvert = \lvert E(S, \bar{S}) \rvert, \sum_{\{ u,v \} \in {n \choose V}} \lvert f(u) - f(v) \rvert = \lvert S \rvert \lvert \bar{S} \rvert\), 显然待证式成立。
Q2
Think about why the above extends to show that
where now the minimum is over \(f : V \to \mathbb{R}\) instead of \(f : V \to \{0, 1\}\).
记 \(R(f)=\frac{\sum_{\{ u,v \} \in E} \lvert f(u) - f(v) \rvert}{\sum_{\{ u,v \} \in {n \choose V}} \lvert f(u) - f(v) \rvert}\), 当 \(f\) 为 \(V \to \{ a,b,c \} (a < b < c)\) 的映射时,其中 \(a,b,c\) 为 \(\mathbb{R}\) 中的常数,记 \(f_{x}\) 为 \(V \to \{ a, x, c \} (a \leq x \leq c)\) 的映射,其中 \(x \in \mathbb{R}\) 为自变量, 可以发现此时 \(R(f_{x})\) 随 \(x\) 单调递增 / 递减:由于 \(\lvert a - x \rvert + \lvert x - c \rvert = a-c\) 互相抵消为常量,\(\lvert a-c \rvert = a-c\) 不变,因此有变化的量只有分子分母中未被抵消的 \(\lvert a-x \rvert\) 与 \(\lvert x-c \rvert\), 因此分子分母都是单调递增或递减的,若二者单调性相反则 \(R(f_{x})\) 单调,若单调性相同,此时二者都是形如 \(y=a-kx\) 的线性函数表达式,即 \(R(f_{x})\) 是两个线性函数的比值,由于分母式会包含分子式,从而分母 \(a,k\) 更大,不难发现此时 \(R(f_{x})\) 是单调递增的,类似的,当分子分母多出来的都是 \(\lvert x-c \rvert\) 时 \(R(f_{x})\) 同样是单调的。
据此可以推出当 \(f\) 的取值多于 \(3\) 个值时,可以在取值区间上找到取值为 \(2\) 个值(记为 \(\{ a,b \}\))的函数 \(f^\ast\) 使得 \(R(f^\ast) \leq R(f)\), 同时用 \(\frac{f^\ast(x) - a}{b - a}\) 代替 \(f^\ast(x)\) 则可以在保持 \(R(f^\ast)\) 不变的情况下将取值改为 \(\{ 0,1 \}\), 因此
Q3
Think about why the above extends to show that
where the minimum is over all functions \(f : V \to \mathbb{R}^k\) for any \(k\).
Hint
You may want to use the inequality that \(\frac{\sum_{i}a_{i}}{\sum_{i}b_{i}} \geq \min_{i} \frac{a_{i}}{b_{i}}\) for \(a_{i}, b_{i} > 0\).
将 \(\frac{\sum_{\{ u,v \} \in E} \lVert f(u) - f(v) \rVert_{1}}{\sum_{\{ u,v \} \in {n \choose V}} \lVert f(u) - f(v) \rVert_{1}}\) 写成 \(\frac{\sum_{\{ u,v \} \in E} \sum_{i} \lvert f_{i}(u) - f_{i}(v) \rvert}{\sum_{\{ u,v \} \in {n \choose V}} \sum_{i} \lvert f_{i}(u) - f_{i}(v) \rvert}\) 然后套不等式 \(\frac{\sum_{i}a_{i}}{\sum_{i}b_{i}} \geq \min_{i} \frac{a_{i}}{b_{i}}\) for \(a_{i}, b_{i} > 0\) 即可。
A Randomized Algorithm¶
基于上面的结果,sparsest cuts 问题转化成了找到 \(f : V \to \mathbb{R}^{k}\) 以最小化
这仍然不是一个简单的 optimization problem. 这里考虑下列可以被 LP 高效解决的 opt prob:
Find values \(d_{u,v} \in \mathbb{R}\) for all \(u \neq v \in V\) to minimize
subject to:
- \(d_{u,v}=d_{v,u} \geq 0\) for all \(u,v\)
- \(d_{u,v}+d_{v,w} \geq d_{u,w}\) for all \(u,v,w\)
- \(\sum_{\{ u,v \} \in {V \choose 2}} d_{u,v}=1\)
也就是给 \(G\) 找一个满足 \(\sum_{\{ u,v \} \in {V \choose 2}} d_{u,v}=1\) 的能使 \(Q(d)\) 最小的 metric \(d\).
有了 metric space \((V, d)\) 就能用 Bourgain's embedding 给出一个 approximation algorithm for sparsest cuts 了。
Q1
Suppose that \(d^\ast\) is the minimizer of the problem above.
Explain why \(Q(d^\ast) \leq \phi(G)\).
对于任意 \(f : V \to \mathbb{R}^k\), 令 \(d_{u,v} = \frac{\lVert f(u) - f(v) \rVert_{1}}{\sum_{\{ u,v \} \in {V \choose 2}} \lVert f(u) - f(v) \rVert_{1}}\), 此时 \(d\) 显然满足条件,且 \(Q(d)=R(f)\), 而又有 \(Q(d^\ast) \leq Q(d) = R(f)\) for all \(f\), 因此 \(Q(d^\ast) \leq R(f^\ast) = \phi(G)\).
Q2
Find a randomized algorithm to approximate \(\phi(G)\). More precisely, give a randomized algorithm that finds \(f : V \to \mathbb{R}^k\) so that, with high probability,
Hint
Your warm-up exercise might be relevant.
Hint
If it comes up, you may assume that Bourgain's embedding works just fine on pseudo-metrics, which are functions \(d(u, v)\) that obey all of the axioms of metrics except that maybe \(d(u, v) = 0\) for \(u \neq v\).
给 \((V, d^\ast)\) 套 Bourgain's embedding 得到 \(f\), 根据 warm-up 中的结论有
Q3
Given \(f\) as in the previous part, explain how to efficiently find a set \(S \subset V\) so that
Hint
Our proof in the first group-work was somewhat algorithmic...
将上一个 group work 中的证明倒过来做一遍,\(f : V \to \mathbb{R}^k\) 转化为 \(f : V \to \{ 0,1 \}\) 然后 \(f(u)=1\) 的点放进 \(S\) 即可。
Optional¶
以下内容来自 DeepSeek R1.
建议与深入思考¶
1. 与其他知识点的联系¶
- Johnson-Lindenstrauss 引理:
- Bourgain 嵌入与 JL 引理均为降维技术,但目标不同:
- JL 引理:保持点对欧氏距离的近似(适用于 \(\ell_2\))。
- Bourgain 嵌入:将任意度量嵌入 \(\ell_1\),适用于更通用的距离结构。
-
对比两者的概率构造方法(随机投影 vs. 随机集合分层采样)。
-
流形学习与降维:
- Bourgain 嵌入可视为一种非线性降维方法,与 Isomap 的思想(通过图度量逼近流形距离)有相似性。
- 讨论如何在流形数据中应用 Bourgain 嵌入。
2. 分层结构的深层意义¶
- 多尺度分析:
- 分层结构(不同层级的集合 \(S_{i,j}\))本质上是对点对距离的“分治”策略:
- 大尺度集合处理近距离点对。
- 小尺度集合处理远距离点对。
-
类似小波变换中的多分辨率分析,不同层级捕捉不同频率的距离信息。
-
与层次聚类的联系:
- 每个层级的集合 \(S_{i,j}\) 可视为对点集的随机聚类中心,嵌入坐标 \(d(x,S_{i,j})\) 反映点与不同聚类中心的关联性。
- 这种构造可启发基于随机投影的层次聚类算法。
3. 算法应用的新视角¶
- 近似稀疏割的改进:
- 在 Sparsest Cuts 问题中,Bourgain 嵌入可替换为更高效的 Chawla-Babai 嵌入(维度 \(O(\log n)\),失真 \(O(\log n)\)),参考 [Abraham et al., 2006]。
-
结合 半定规划(SDP):通过 SDP 松弛优化度量 \(d^*\),再嵌入到 \(\ell_1\),提升近似比。
-
动态网络路由:
- Bourgain 嵌入可用于设计紧凑的路由表:将节点映射到低维空间,路由决策基于嵌入坐标的局部性。
- 例如,在分布式系统中,利用嵌入坐标的 \(\ell_1\) 距离快速定位最近服务节点。
关键公式与定理的再验证¶
1. Bourgain 嵌入的失真分析¶
- 核心步骤:
- 对每个点对 \((x,y)\),存在层级 \(i\) 使得至少 \(c \log n\) 个集合 \(S_{i,j}\) 满足:
\(\(|d(x,S_{i,j}) - d(y,S_{i,j})| \geq \Omega\left( \frac{d(x,y)}{\log n} \right).\)\) - 总 \(\ell_1\) 距离贡献为 \(\sum_{i,j} |d(x,S_{i,j}) - d(y,S_{i,j})| \geq \Omega(d(x,y))\),但需注意归一化因子(缩放 \(\beta\))的影响。
2. Sparsest Cuts 的算法正确性¶
- 从嵌入到割集:
- 选择随机坐标 \(k\) 和阈值 \(\theta\),定义割集 \(S = \{ x \mid f(x)_k \leq \theta \}\)。
- 通过 线性代数技巧:\(\ell_1\) 距离的期望贡献与割的稀疏性直接相关,需验证:
\(\(E[\phi(G,S)] \leq O(\log n) \phi(G).\)\)
怎么想到 Sparsest Cuts to Metrics 这样的转换?¶
- 松弛以利用连续工具:将离散的集合选择转化为函数优化,绕过组合复杂性。
- 几何嵌入的类比:借用 Bourgain 等嵌入技术,将抽象度量转换为几何空间中的点。
- 对偶性与线性规划:通过 LP 松弛找到最优伪度量,再嵌入为几何结构。
- 随机化与概率方法:利用高维空间中的随机投影和阈值切割,保证近似比。
- 历史范式的延续:ARV 等算法的成功案例推动类似方法在 Sparsest Cut 中的应用。
这种转换的本质是将 组合难题 重新参数化为 连续优化+几何分析+概率舍入 的联合框架,是理论计算机科学中“将困难问题嵌入友好空间”这一核心策略的典型体现。
-
Ittai Abraham, Yair Bartal, and Ofer Neiman. Advances in metric embedding theory. In Proceedings of the thirty-eighth annual ACM symposium on Theory of computing, pages 271-286, 2006. ↩