Decidability

为什么要学习 unsolvability:

• 在找到一个 algorithmic solution 之前明白这个 problem 必须被简化/修改
• 尽管求解的是 solvable problems, 考虑它是否是 unsolvable 的过程可以激发求解它的 insights

Decidable Languages

Decidable problems concerning regular languages

我们从与 finite automata 有关的 computational problems 出发.

Acceptance problem

Acceptance problem for DFAs 是检测某个 DFA 能否 accept 给定的 string, 这个问题可以被表达成一个 language \(A_{\textsf{DFA}}\). 这个 language 包含了所有 DFA 与它能 accept 的 strings:

\[A_{\textsf{DFA}}=\{\langle B, w \rangle | B \text{ is a DFA that accepts input string }w\}.\]

类似地, 也有 acceptance problem for NFAs 和 \(A_{\textsf{NFA}}\):

\[A_{\textsf{NFA}}=\{\langle B, w \rangle | B \text{ is an NFA that accepts input string }w\}.\]

以及 for regular expressions \(A_{\textsf{REX}}\):

\[A_{\textsf{REX}}=\{\langle R, w \rangle | R \text{ is a regular expression that generates string }w\}.\]

Theorem

\(A_{\textsf{DFA}}, A_{\textsf{NFA}}, A_{\textsf{REX}}\) are decidable languages.

Proof

Proof idea 是构造一个 TM \(M\) that decides \(A_{\textsf{DFA}}\)/\(A_{\textsf{NFA}}\)/\(A_{\textsf{REX}}\).

\(M\) = "On input \(\langle B / R, w \rangle\), where \(B / R\) is a DFA/NFA/REX and \(w\) is a string:

1. Simulate \(B / R\) on input \(w\).
2. If the simulation ends in an accept state, accept. If it ends in a nonaccepting state, reject."

Emptiness testing

Emptiness testing for the language of a finite automaton 是检测一个 finite automaton 是否任何 string 都不 accept 的问题. 它同样也表达为 language 的形式:

\[E_{\textsf{DFA}} = \{\langle A \rangle | A \text{ is a DFA and } L(A)=\emptyset\}\]

Theorem

\(E_{\textsf{DFA}}\) is a decidable language.

令

\[EQ_{\textsf{DFA}} = \{\langle A, B \rangle | A \text{ and } B \text{ are DFAs and } L(A)=L(B)\},\]

我们有

Theorem

\(EQ_{\textsf{DFA}}\) is a decidable language.

Decidable problems concerning context-free languages

类似地, 我们定义以下 languages:

\[ \begin{aligned} A_{\textsf{CFG}} &= \{\langle G, w \rangle | G \text{ is a CFG that generates string } w\},\\ E_{\textsf{CFG}} &= \{\langle G \rangle | G \text{ is a CFG and } L(G) = \emptyset\},\\ EQ_{\textsf{CFG}} &= \{\langle G, H \rangle | G \text{ and } H \text{ are CFGs and } L(G)=L(H)\}. \end{aligned} \]

它们都是 decidable languages.

Theorem

\(A_{\textsf{CFG}}, E_{\textsf{CFG}}, EG_{\textsf{CFG}}\) are decidable languages.

Theorem

Every context-free language is decidable.

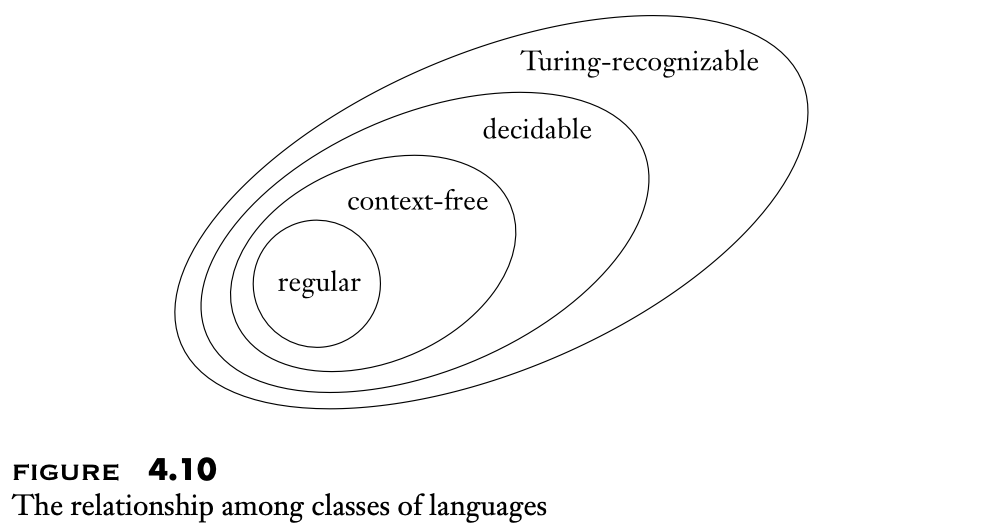
Undecidability

本节我们介绍计算理论中最 philosophically important 的定理之一: There is a specific problem that is algorithmically unsolvable.

令

\[A_{\textsf{TM}} = \{\langle M, w \rangle | M \text{ is a TM and } M \text{ accepts }w\},\]

与前面的 DFA, CFG 不同, 它是 undecidable 的.

Theorem

\(A_{\textsf{TM}}\) is undecidable.

不难发现 \(A_{\textsf{TM}}\) 是 Turing-recognizable 的, 下列 Turing machine \(U\) recognizes \(A_{\textsf{TM}}\):

\(U\) = "On input \(\langle M, w \rangle\), where \(M\) is a TM and \(w\) is a string:

1. Simulate \(M\) on input \(w\).
2. If \(M\) ever enters its accept state, accept; if \(M\) ever enters its reject state, reject."

可以 simulate 任何其他 Turing machine 的 machine 称为 universal, \(U\) 就是一个 universal Turing machine.

The diagonalization method

这一部分主要介绍 Cantor 提出的 可数集/不可数集 的概念.

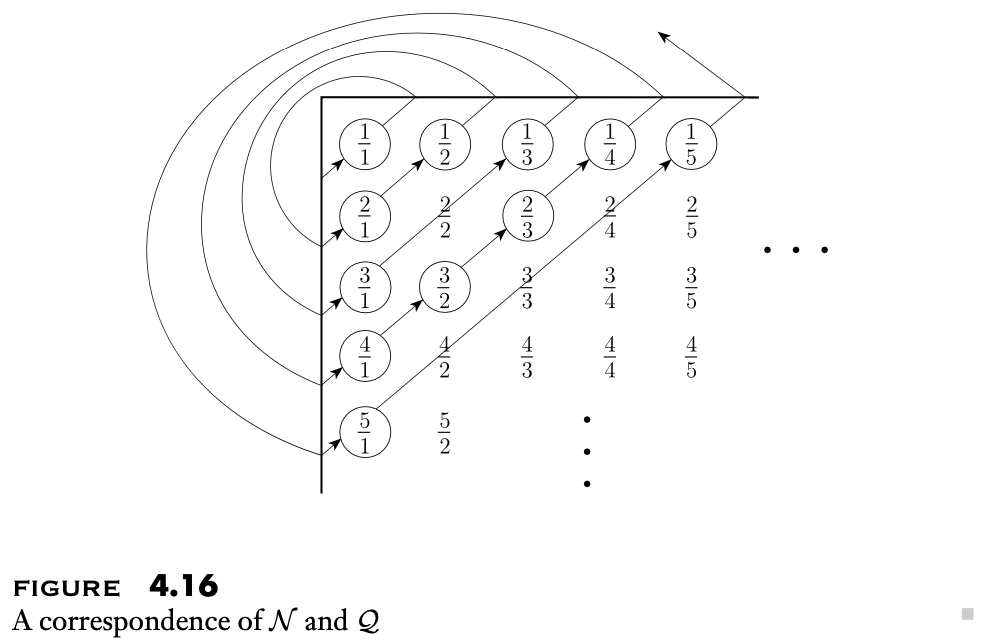
基于这个概念, 我们可以发现不是所有的 languages 都是 Turing-recognizable 的.

Theorem

Some languages are not Turing-recognizable.

A Turing-unrecognizable language

co-Turing-recognizable

We say that a language is co-Turing-recognizable if it is the complement of a Turing-recognizable language.

Theorem

A language is decidable iff it is Turing-recognizable and co-Turing-recognizable.

Corollary

\(\overline{A_{\textsf{TM}}}\) is not Turing-recognizable.